What is the Annual Rate Approximation?
The annualized rate is a standardized method to express the rate of change or growth of an investment or financial variable over a specific period as if it were compounded annually. It takes into account the Time Value of Money (TVM) to demonstrate the value of your ESPP on the purchase date. It enables you to compare contributions to an ESPP with another type of investment vehicle, including savings accounts.
Notice: The annual rate for most ESPPs may appear naturally high due to the unique functionality and discount offered. ESPPs involve regular contributions over time, culminating in a single lump sum significantly greater than your cumulative contributions on the purchase date.
Calculating Annualized Rate
The calculator uses the XIRR function (EXtended Internal Rate of Return) to determine the annualized rate.
Currently, this calculator assumes semi-monthly contributions of the same amount based on the total contribution amount starting after the offering date and up until the purchase date. It attempts to use realistic paydays, avoiding weekends.
Examples
Let's look at an example to illustrate the calculation of the Annual Rate.
In this scenario, we'll consider a bi-monthly contribution of $1,000 over a 6-month period, from February to August, assuming the stock price remains unchanged or decreases. As a result, the return will be the minimum amount, which would be approximately 17.65% based on a 15% discount from the lowest purchase price.
On the left, you will find the calculated annual rate on the purchase date, while on the right, the calculated annual rate after one year.
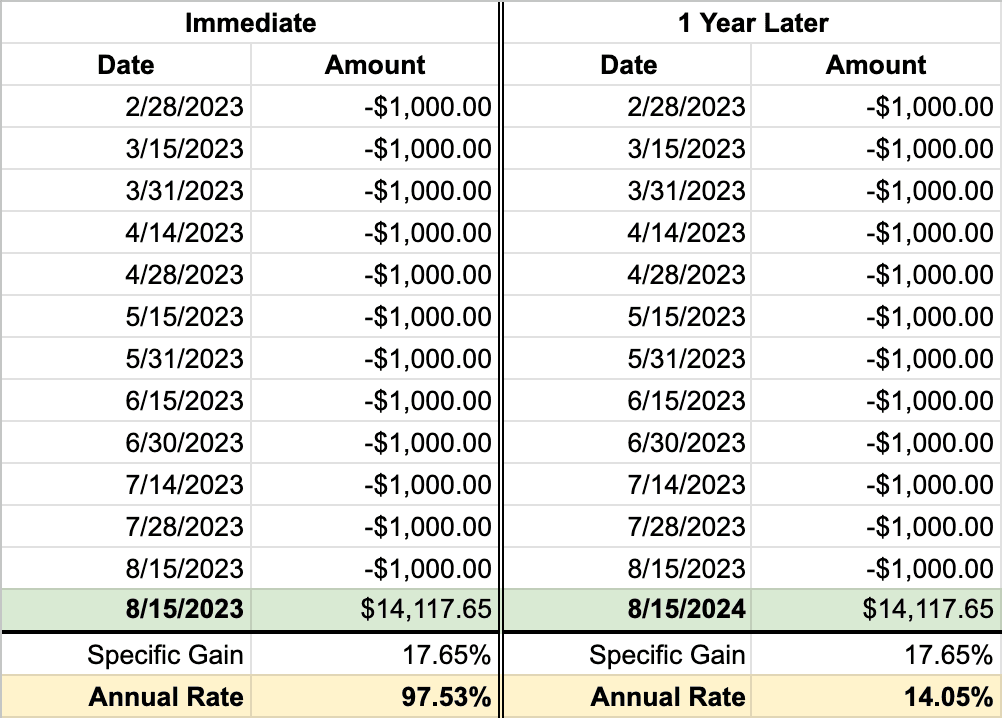
You will notice that the annual rate on the purchase date appears significantly higher than the actual gain. This phenomenon is due to the calculation considering both the contribution timings and assumes that everything is sold on the purchase date. If you decide to wait a year to sell the shares, and assuming the stock price remains unchanged, the annual rate will actually be lower than the gain.
Now, let's consider another scenario where we maintain the same contribution rate as above, but this time, the stock price doubles by the purchase date:
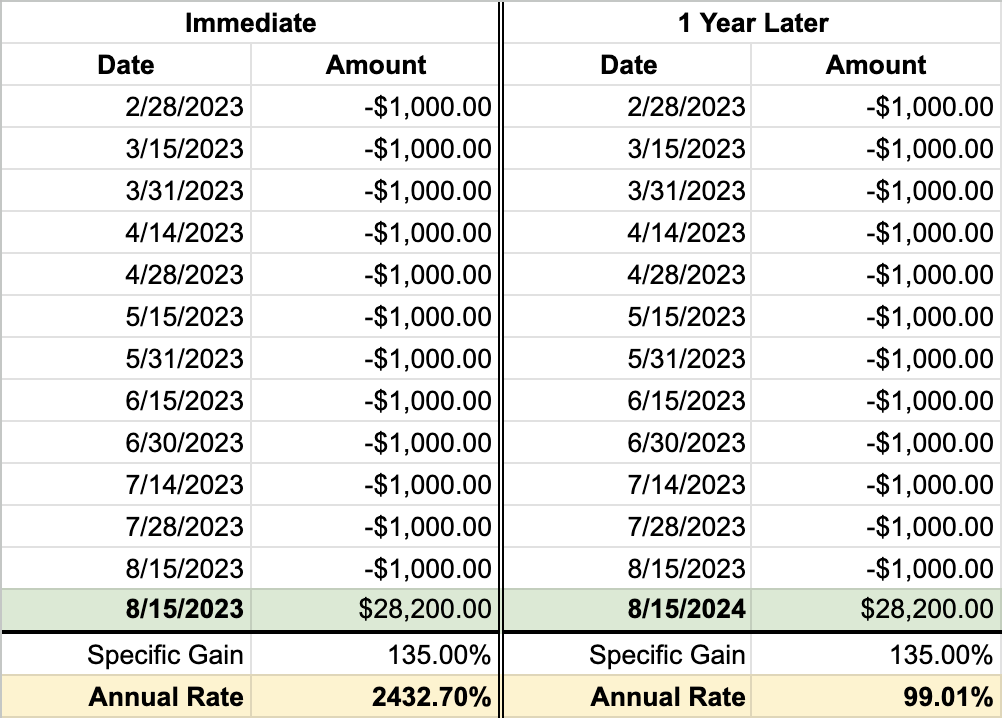
Wow! The annualized rate on the purchase date looks incredible, right? But over time, assuming the stock price remains constant, the annual rate will gradually decrease. Similarly to the previous example, waiting a year will result in the annual rate being less than the actual gain.
It's essential to understand that this doesn't imply an immediate sell-off. Rather, it emphasizes that the annual rate shouldn't be the sole metric you consider when evaluating your investment. Other factors, such as long-term performance, market trends, and individual financial goals, should also play a significant role in your decision-making process.
Conclusion
The annual rate for ESPPs serves as a valuable comparative metric, enabling investors to gauge the performance of these plans in relation to other investment options. The examples presented highlight the inherent attractiveness of ESPPs as an investment opportunity, showcasing their potential for high returns. As with any investment, it is crucial to consider individual financial goals and risk tolerance while appreciating the benefits of ESPPs as an amazing opportunity for long-term financial growth.